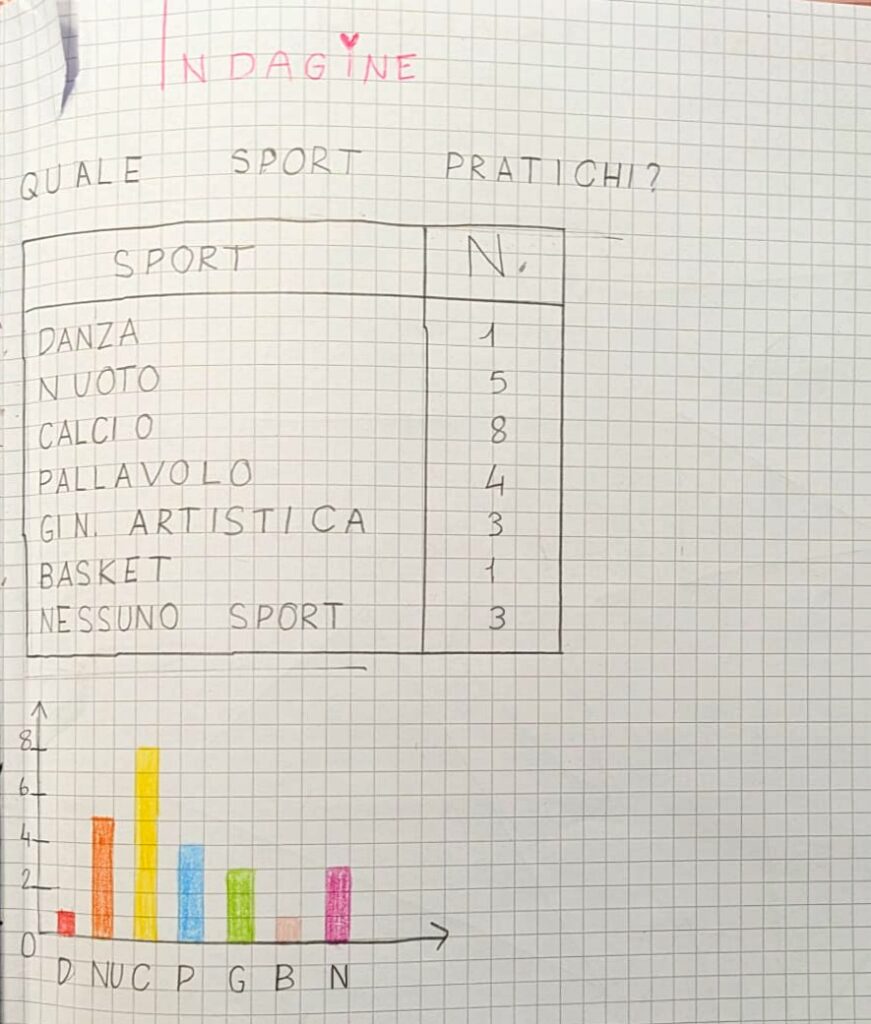
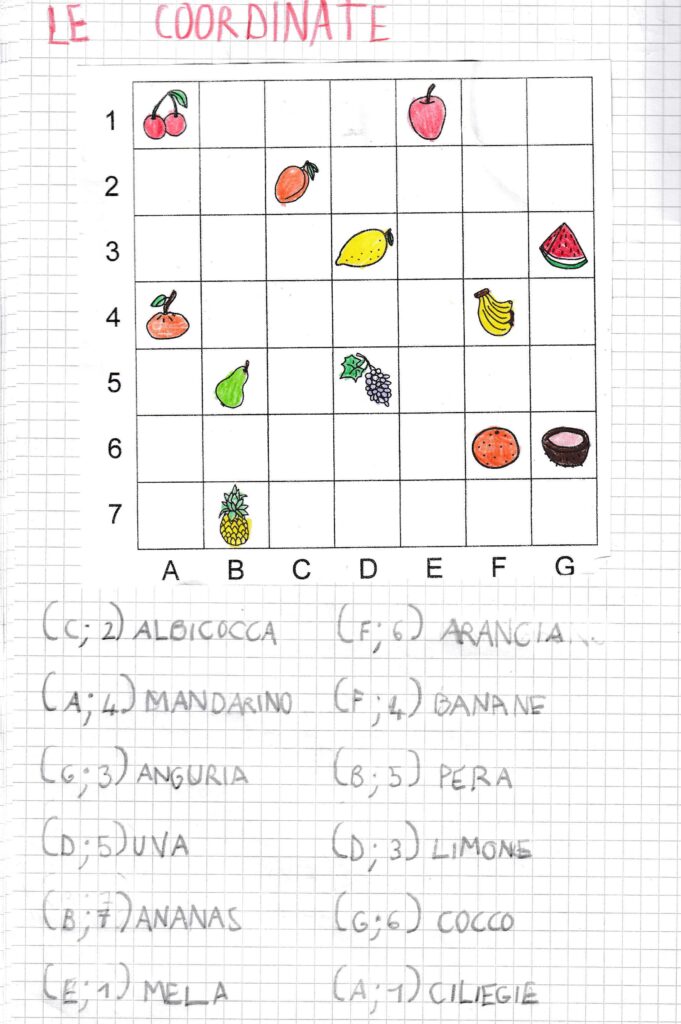
Oggi pomeriggio abbiamo iniziato ripassando le tabelline dello 0, dell’1 e del 2.

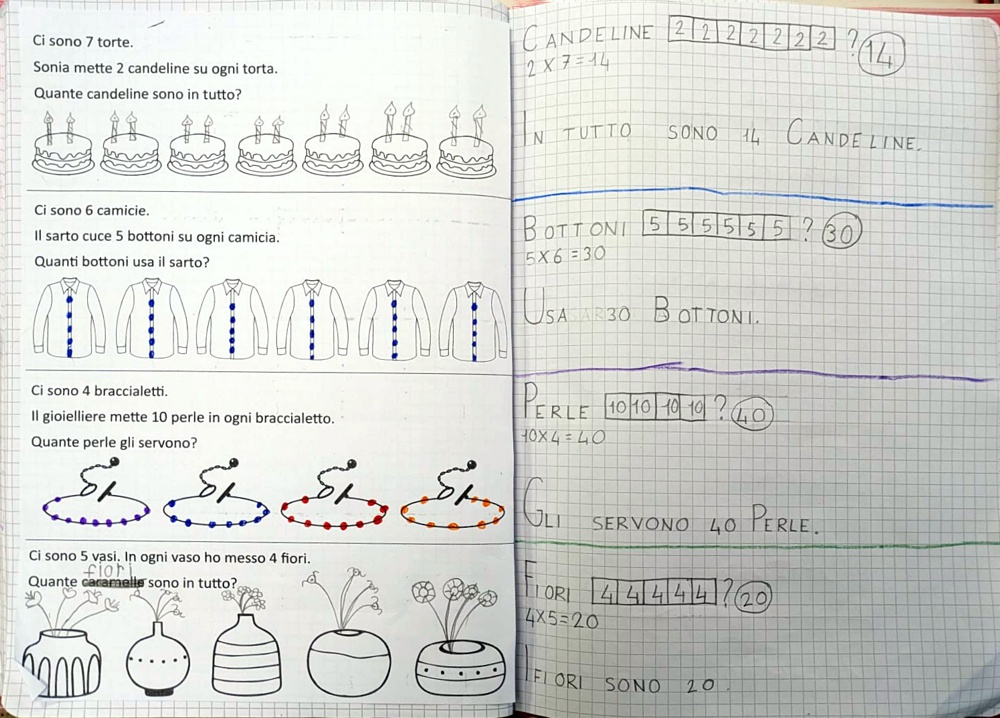
Poi abbiamo lavorato su questa scheda, che ho usato per presentare i primi problemi di moltiplicazione. Abbiamo ragionato sul fatto che le moltiplicazioni rappresentano addizioni ripetute, quindi potevamo usare la barra dell’addizione. Quindi abbiamo disegnato una barra aperta in fondo (perchè non sapevamo quanto doveva essere lunga). Poi abbiamo cominciato a ragionare sui numeri e su come sistemarli. La discussione è stata molto interssante.

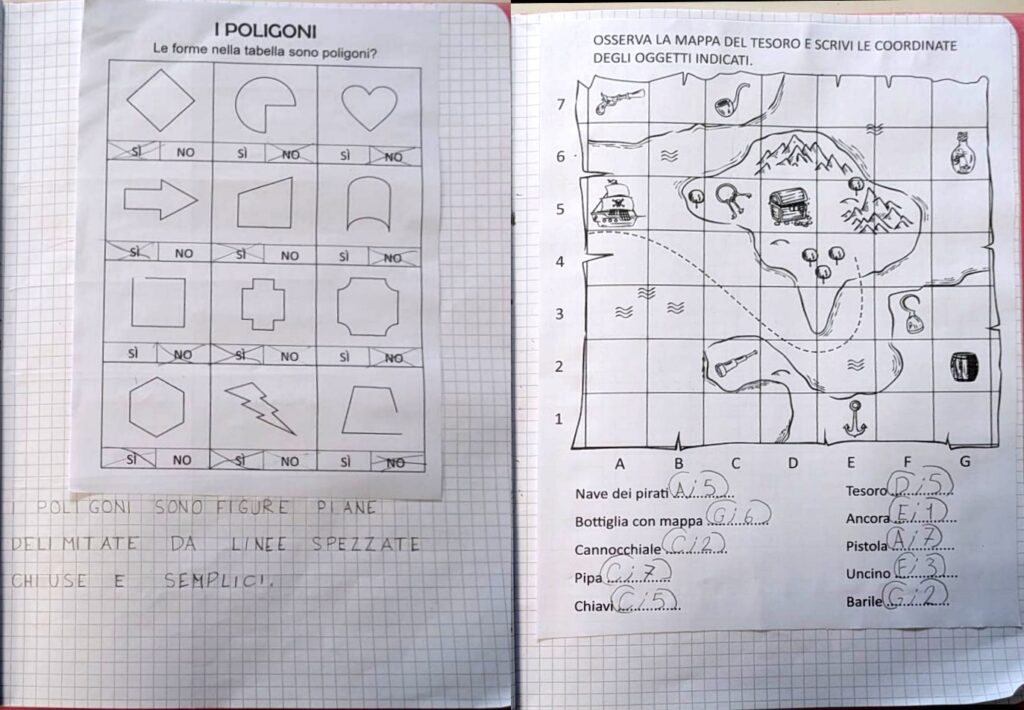
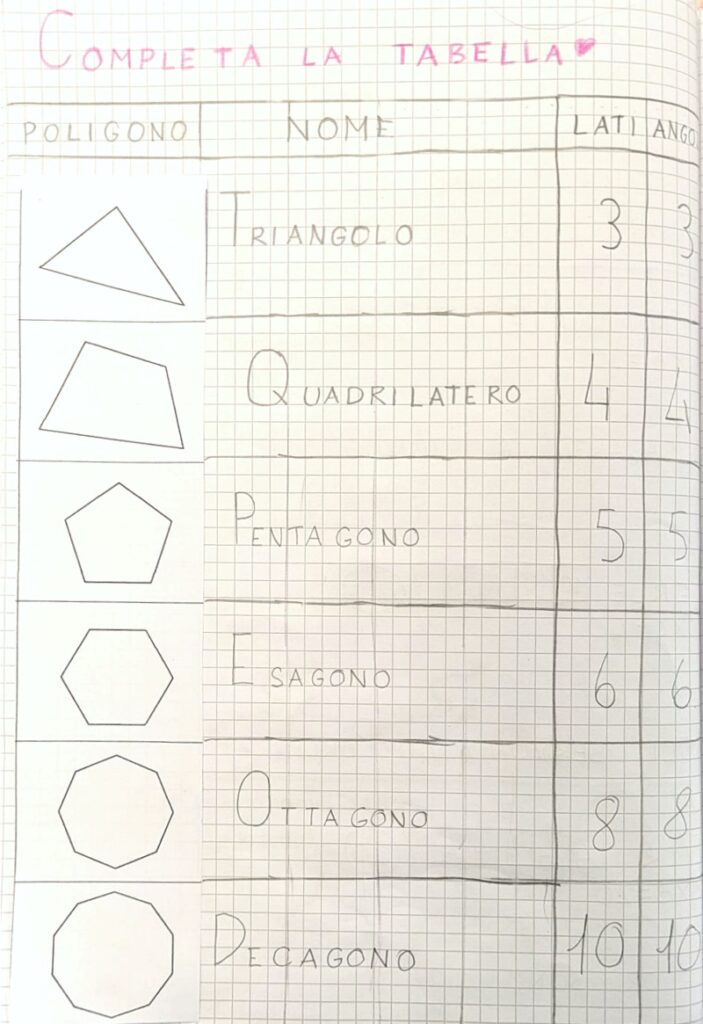
Siamo riusciti a trovare il tempo per ripassare i nomi dei poligoni in base al numero di lati e angoli, con questa tabella.

Compito di casa: studiare la tabellina del 2 e i nomi dei poligoni.

Oggi pomeriggio i bambini hanno risolto in coppia questa scheda di problemi di addizione e sottrazione. Pensavo che avrebbero trovato delle difficoltà nel secondo problema, invece hanno fatto maggiori errori nel terzo problema, che è di differenza.

Hanno poi risolto delle operazioni in colonna. Mi è “scappata” la centinaia nella prima addizione, l’abbiamo risolta così.

Poi abbiamo svolto una delle cinque indagini proposte dal nostro libro di testo.

Stamattina abbiamo iniziato con la tabellina del 2. Dopo averla scritta e rappresentata con i rettangoli, l’abbiamo studiata insieme. I bambini hanno anche colorato questo puzzle, che proviene dal libro “The Multiplication Tables Colouring Book” di  Heather McElderry. Comprai il libro nel 1996 a Londra e lo usai con diverse classi. Sarebbe stato ottimo averlo quando studiavamo le numerazioni, ma l’ho trovato solo in questi giorni, dopo averlo perso di vista da diversi anni. Si trova ancora in commercio. La cosa simpatica è che i puzzle da colorare sono fatti benissimo, non si indovina assolutamente l’immagine che emergerà.

Sul libro di testo abbiamo completato una pagina sulle figure piane.

Poi abbiamo lavorato su queste due pagine del libro. Fin dalla prima abbiamo realizzato qualche istogramma, quando se ne prsentava l’opportunità. Nei prossimi mesi ci dedicheremo più assoduamente a questo argomento, considerato che ci sono almeno 3-4 quiz sugli istogrammi o gli ideogrammi nelle Prove INVALSI.

Ripassiamo la tabellina dello 0, elemento assorbente della moltiplicazione. Poi cominciamo a ragionare sull’1. Scriviamo la tabellina dell’1 e la rappresentiamo con i rettangoli.

Poi completiamo una scheda con gli schieramenti, scrivendo le due moltiplicazioni.

Stamattina abbiamo iniziato con la tabellina dello 0, di cui avevamo parlato nei giorni scorsi in classe. Quando si lavora con rettangoli, schieramenti, disegni lo 0 non compare mai, ovviamente. Però la questione dello 0 è venuta fuori e avevamo già riflettuto che, mentre nell’addizione e nella sottrazione lo 0 è l’elemento neutro, nella moltiplicazione ha tutto un altro ruolo e diventa l’elemento assorbente.

Abbiamo proseguito con la moltiplicazione usando questa scheda, che ho un po’ rinnovato, ma che ormai per me è un classico. Lavoriamo insieme sui primi due disegni, poi i bambini proseguono da soli e correggiamo insieme alla fine.

Sul libro di testo ripassiamo le linee aperte/chiuse e curve/spezzate/miste. Poi ripassiamo la definizione dei poligoni e i nomi dei poligono in base ai lati/angoli. Proseguiamo con una scheda molto facile di riconoscimento dei poligoni. Sotto alla scheda copiamo la definizione di poligono del nostro libro di testo, che dobbiamo imparare a memoria (entro la quinta).

Concludiamo con un esercizio veloce sulle coordinate, che i bambini hanno svolto in autonomia.

Stamattina abbiamo lavorato tantissimo. Prima di tutto abbiamo completato una pagina del libro per ripassare la defnizione di poligono.

Poi abbiamo fatto gli ultimi esercizi del libro sulle coordinate. Considerato che c’è sempre un quiz INVALSI nelle prove di matematica di seconda, nei prossimi mesi proporrò vecchi quiz INVALSI per tenerci in allenamento.

Abbiamo lavorato sulla moltiplicazione, utilizzando un’immagine modificata di Math Talk che non avevamo usato l’anno scorso. I bambini hanno subito trovato le addizioni ripetute. Abbiamo scritto anche un’addizione non ripetuta, per ricordarci che NON può essere trasformata in una moltiplicazione. Le scritte sul quaderno sono in English, perchè proprio in questi giorni abbiamo inziato una Unit sulla fattoria.

Ultima attività, una scheda di calcolo a mente per tenerci in esercizio. I bambini hanno lavorato autonomamente e abbiamo corretto alla lavagna.

Compito di casa: imparare la numerazione del 10 (la sanno già) e calcolo in colonna.

Oggi pomeriggio abbiamo lavorato su:

• una strategia di calcolo della sottrazione (amico del 10 per le unità e una decina in meno);
• la moltiplicazione con gli schieramenti quadrati;
• le coordinate, dove abbiamo disegnato la griglia e scritto le coordinate, poi i bambini hanno colorato i quadrati giusti.

Stamattina abbiamo lavorato sul quaderno, rappresentanto degli schieramenti rettangolari con addizioni ripetute e moltiplicazioni. Dopo aver fatto il primo esempio, i bambini hanno proceduto in autonomia.

Proseguiamo con un’attività sul reticolo, in cui i bambini devono individuare l’oggetto abbinato alle coordinate.

Anche oggi abbiamo avuto diversi assenti. Ho iniziato il ripasso di geometria dalle linee, prima sul libro e poi sul quaderno.

Cominciamo ad avere numerosi assenti per l’influenza stagionale, quindi stamattina abbiamo ripassato qualche strategia di calcolo e problemi ma solo a livello orale.

Insieme abbiamo completato una pagina sulla moltiplicazione del libro di testo. In geografia ho introdotto il reticolo, che ricorre spesso nelel prove INVALSI di matematica di seconda e quindi ci lavoreremo un po’ sopra.