Oggi pomeriggio ho cominciato a guardare con i miei alunni il fascicolo delle prove INVALSI dell’anno scorso, proiettandolo sulla digital board. Abbiamo fatto insieme anche alcuni quiz (D1, D2, D7, D24, D25, D26) abbastanza facili e adatti ad essere risolti semplicemente guardando la digiral board.

Sto cercando di far ragionare i miei alunni sul fatto che mettere in campo tutte le strategie possibili è importantissimo, ma con bambini di 7-8 anni non è facile.

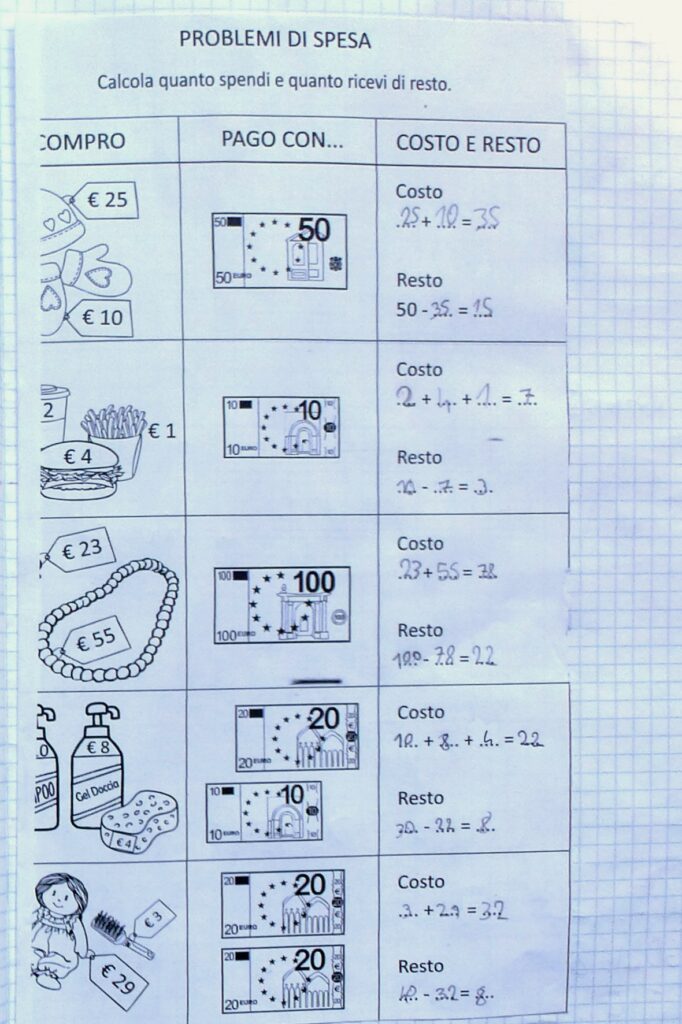
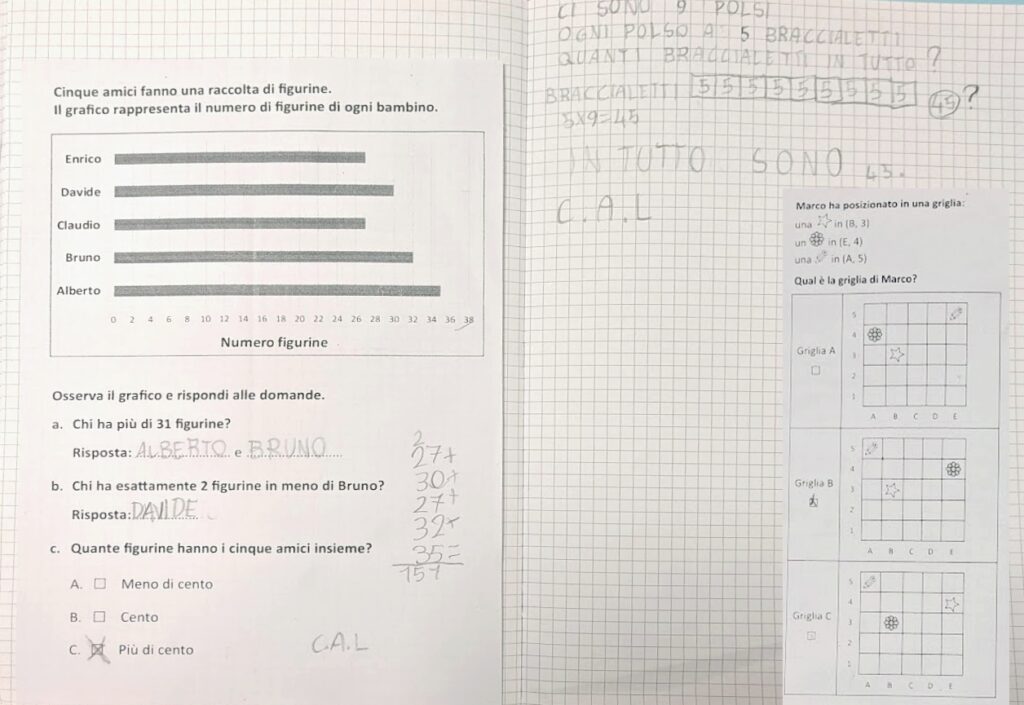
Prendo come esempio questo quiz:

Appena l’ho proiettato, hanno tutti cominciato a contare, ma dopo poco si sono fermati e hanno ricordato quando in prima, dovendo contare gruppi di oggetti sul libro di testo, avevamo imparato a fare un puntino o una crocetta su ogni oggetto, in modo da non lasciarsi sfuggire qualcosa. A quel punto abbiamo ricominciato a contare “marchiando” ogni sassolino ed è apparso ovvio a tutti che la risposta giusta è la B.

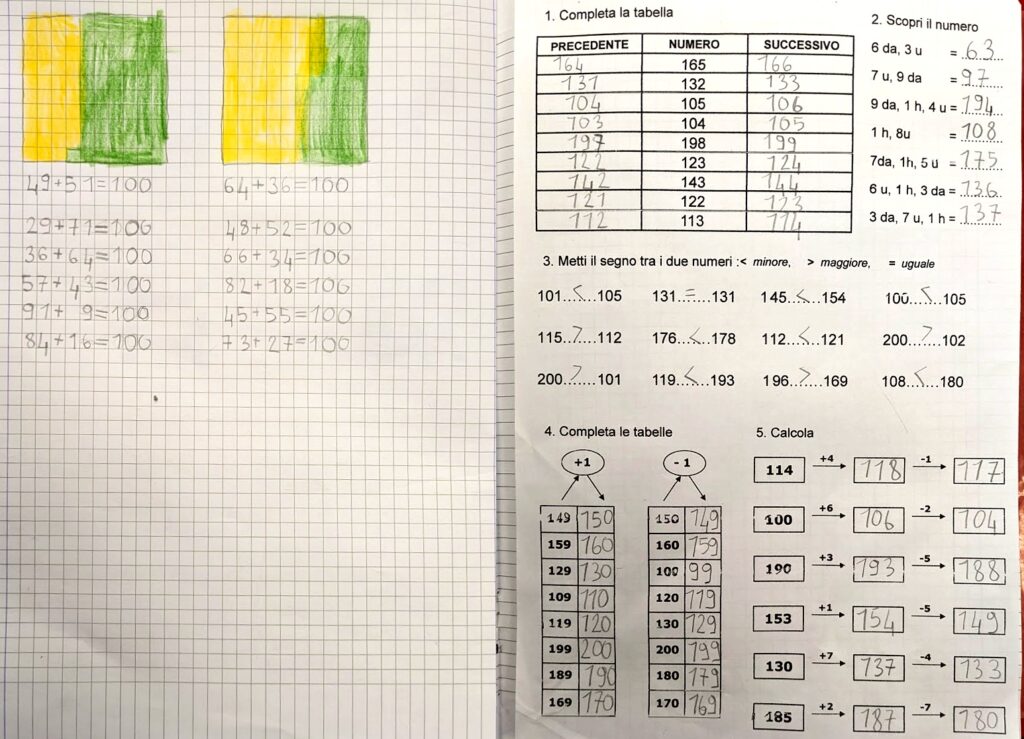
Nelle prove INVALSI ci sono diversi argomenti che ritornano ogni anno (istogrammi, orologio, simmetria, reticolo, ecc.). C’è sempre, ad esempio, un esercizio sulla linea dei numeri. Cominciamo a lavorare sul quaderno, dove propongo tre esercizi sulla linea dei numeri presi dai fascicoli degli ultimi tre anni. A destra i quiz originali, a sinistra gli stessi quiz riportati sul quaderno.

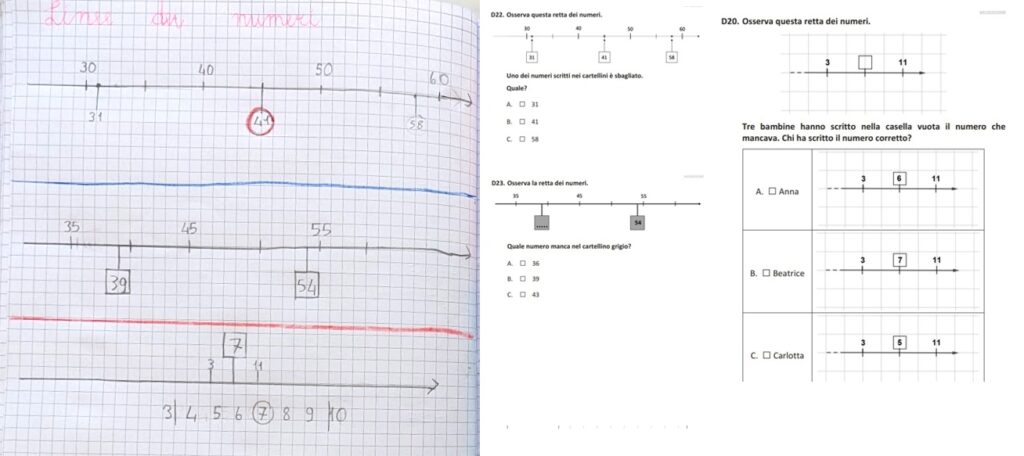
I primi due quiz sono abbastanza simili. La difficoltà è capire il valore delle linee intermedie tra 30-40-50-60 nel primo esercizio e 35-45-65 nel secondo esercizio. La maggior parte dei miei alunni ha saputo risolvere i due quiz e motivare la soluzione.

Il terzo quiz è micidiale. Infatti solo 5 bambini su 22 lo hanno risolto correttamente scegliendo il 7; alla richiesta di motivare la loro scelta, hanno affermato che hanno scelto a caso. La maggior parte ha scelto 6 con motivazioni che francamente ho faticato a capire. Nessuno ha scelto 5: partendo da 3 e contando i due quadretti successivi si arriva a 5, ma continuando a contare i quadretti successivi si arriva a 7, non a 11. Forse per questo motivo il 5 è stato scartato da tutti.

Per dimostrare alla classe che la soluzione corretta è 7 ho chiesto ai bambini di trovare un modo, una strategia o un’idea, ma non è venuto fuori nulla. Allora ho fatto scrivere i numeri da 3 a 11. Appena li abbiamo scritti, il 7 si è subito evidenziato come il numero centrale e perciò quello da scrivere nel quadretto vuoto. Speriamo che quiz così astrusi non ci siano più.

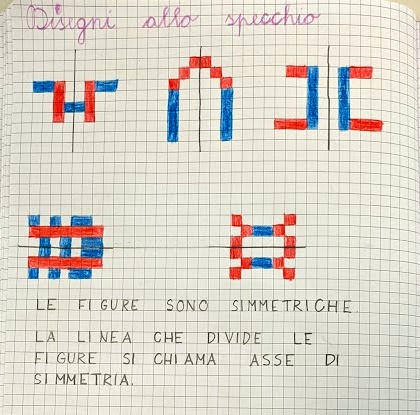
Abbiamo lasciato le prove INVALSI e ci siamo dedicati alla simmetria. Ho seguito di nuovo le indicazioni della guida Maematica PERCONTARE 2, utilizzando dei rettangoli di carta, sui quali i bambini:

• hanno fatto una piega
• hanno ripassato la piega/asse di simmetria tracciando una linea con il righello
• disegnato la metà di una figura fatta solo da segmenti (no linee curve)
• usato uno spillo per riportare sull’altra metà del foglio i vertici
• unito con il righello e la matita i buchini prodotti dallo spillo.

Questo è stato il lavoro sulla simmetria più difficile fatto finora, ma è stato capace di coinvolgere moltissimo tutta la classe, anche se qualcuno si è perso a infilzarsi la pelle con lo spillino. Alcuni bambini hanno fatto molta fatica ad utilizzare i buchini per disegnare la parte simmetrica, altri hanno capito perfettamente e hanno prodotto diversi lavori.

Oggi i miei alunni si sono esercitati con dei problemi di addizione, sottrazione e moltiplicazione.

Poi abbiamo ripassato le tabelline e concluso con il calcolo in colonna.

Oggi siamo stati impegnati con il progetto “Orto in cassetta” quindi siamo riusciti solo a completare una scheda con gli euro e l’esercizio con le moltiplicazioni in colonna dlla scheda.

Proseguiamo con il lavoro sulla simmetria ritagliando figure su pezzi di cartoncino colorato, che incolliamo sul quaderno. Ogni bambino ha sviluppato le sue idee, ma si sono anche molto influenzati gli uni con gli altri.

Iniziamo ripassando insieme la tabellina del 6 e facendo la gara.

Poi ripassiamo gli amici del 100, che avevamo trascurato, e completiamo una scheda sui numeri da 100 a 200.

Risolviamo otto operazioni in colonna per esercitarci e completiamo un quiz sul reticolo e un quiz sugli istogrammi di vecchie Prove IVALSI.

Stamattina abbiamo ripassato le tabelline del 2, 3, 4, 5, 6 e fatto questa verifica delle tabelline del 2, 3 e 4. La verifica è andata molto bene, i miei alunni si stanno impegnando molto.

Ho rispiegato le moltiplicazioni in colonna, perchè è rientrata dalla malattia una bambina, e ci siamo esercitati un po’.

Abbiamo concluso con l’introduzione alla simmetria. Abbiamo disegnato insieme la prima figura, tratta dalla guida “Matematica PerContare 2”, poi ho dato ai bambini degli specchietti che hanno appoggiato sull’asse di simmetria per vedere “come veniva” e infine hanno riprodotto l’immagine simmetrica. Abbiamo lavorato in questo modo per tutte le figure.

Oggi pomeriggio gara di tabelline, poi abbiamo lavorato sulle moltiplicazioni in colonna.

Stamattina abbiamo rappresentato sul quaderno la tabellina e i rettangoli del 6.

Poi abbiamo lavorato sulla moltiplicazione, riprendendo il lavoro di ieri mattina.

Riprendiamo il lavoro di ieri con un lavoro sui rettangoli.

Ripassiamo le tabelline e facciamo la solita gara.

Stamattina abbiamo ripassato le tabelline, poi ho introdotto la moltiplicazione in colonna.

Sono partita dal rettangolo di 12×3, seguendo le linee guida del Progetto PerContare.Ho chiesto ai miei alunni come potevamo procedere, visto che non conosciamo la tabellina del 12. Da questo è partita una discussione matematica un po’ moscia, non venivano fuori idee di nessun tipo, nemmeno quella di contare i quadretti all’interno del rettangolo.

A quel punto ho proposto io di tagliare il rettangolo e da lì la discussione si è fatta un po’ più animata. Alla fine, dopo 4 tagli, abbiamo ragionato sul fatto che il taglio che rende i calcoli più facili è quello 10+2, perchè nel nostro sistema decimale e posizionale è sempre vantaggioso nel calcolo separare le decine dalle unità.

Dopo il lavoro sul rettangolo 12×3 i bambini hanno completato una scheda sui numeri da 100 a 200.

Come ogni settimana ho proposto ai miei alunni anche dei vecchi quiz INVALSI sul reticolo e sugli istogrammi. E per concludere abbiamo anche risolto un problema inventato giorni fa.