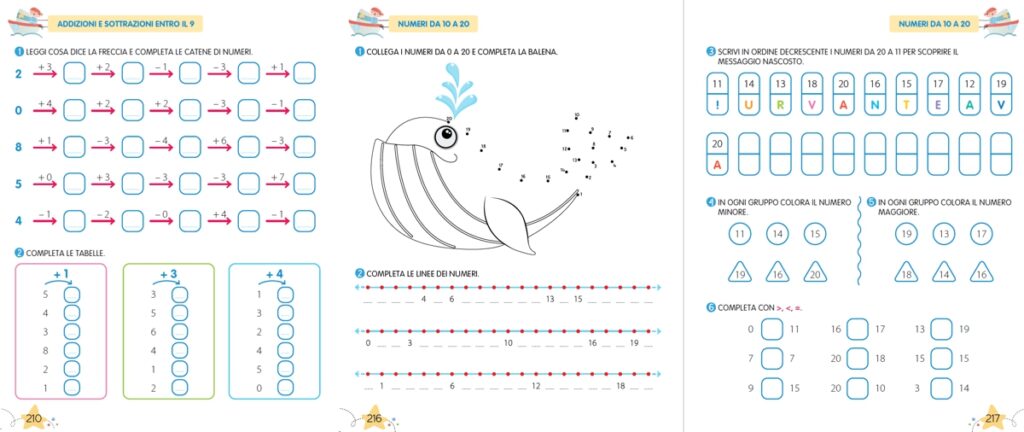
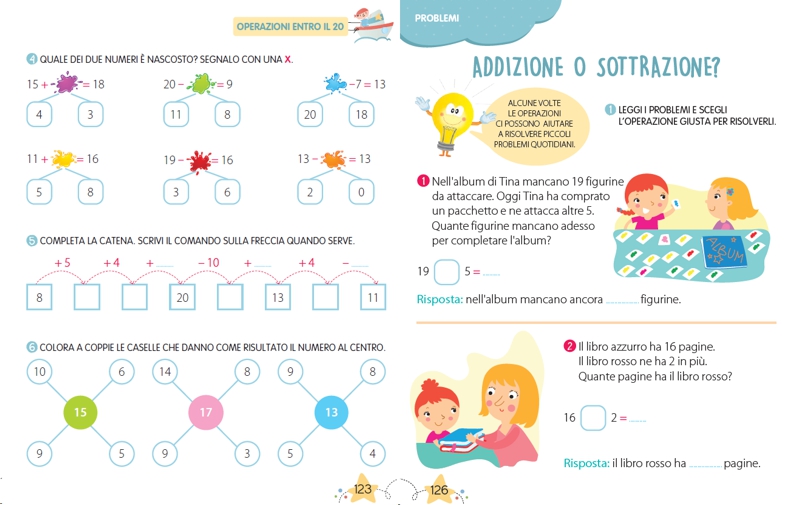
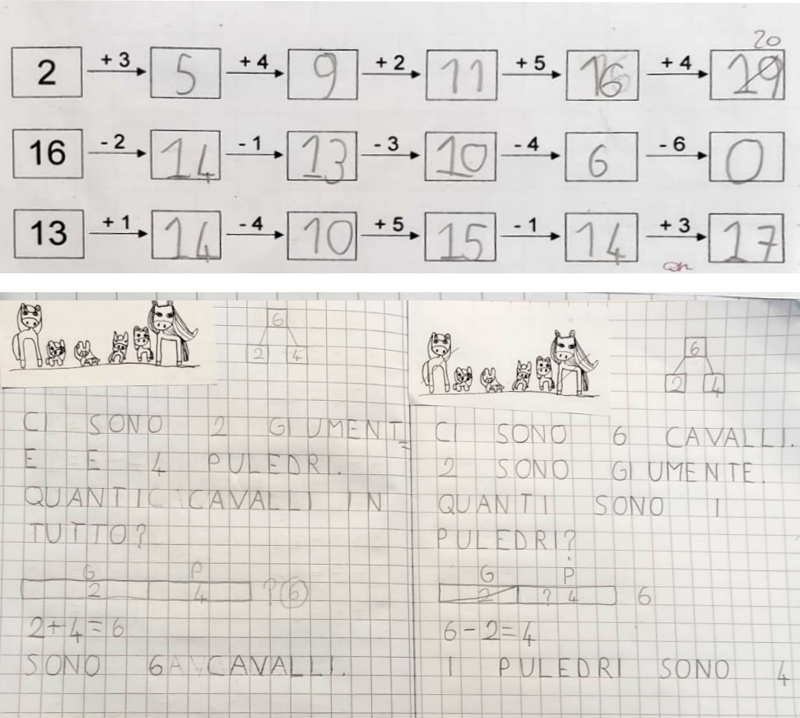
Oggi pomeriggio ho ritirato le linee dei numeri da 0 a 20 e consegnato la tabella del 30, che ho fotocopiato su cartoncino e che i bambini terranno nella copertina del quaderno, in modo da poterla utilizzare quando ne hanno bisogno.
Abbiamo lavorato insieme sulla tabella, per capire come funziona, dato che è un po’ diversa dalla linea del 20 (non c’è lo 0, si deve saltare nei quadretti, ecc.). In particolare abbiamo provato a contare avanti e indietro per capire bene come “si va a capo”.
Poi sul quaderno abbiamo costruito 4 tabelle, che i bambini hanno potuto completare in autonomia, usando la tabella del 30 quando lo ritenevano necessario, per calcolare:
- +1 (un salto a destra)
- -1 (un salto a sinistra)
- +10 (un salto in basso)
- -10 (un salto in alto).