Sempre in attesa che tornino gli assenti, oggi pomeriggio abbiamo lavorato su un problema di questa scheda. Tutti hanno capito come svolgere il lavoro e come trasformare la "storia disegnata" in una "storia di numeri".

Come compito ho assegnato due esercizi online: completamento di linee dei numeri e addizioni. Tutti i miei alunni possono connettersi con computer, tablet o telefono e quindi sto sfruttando questa opportunità.

Questa mattina ero pronta a presentare la decina, ma con tre bambini assenti ho preferito aspettare.

Abbiamo perciò costruito e risolto un'altra tabella dell'addizione.

Poi abbiamo risolto gli ultimi due problemi della scheda: sul primo abbiamo lavorato insieme, perchè presenta due storie di numeri, cioè bambini e palloni; il secondo sugli uccellini è stato risolto individualmente.

Infine abbiamo completato una pagina del libro giallo, che avevamo un po' abbandonato.

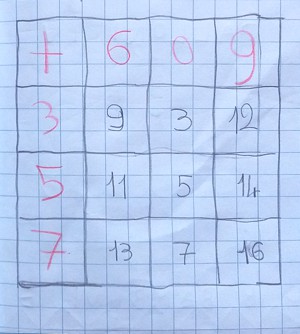
Questa mattina ho presentato ai bambini una scatola con circa 500 cannucce. Ho chiesto a ciascuno di indovinare il numero delle cannucce e sono venuti fuori i numeri più disparati, da 100 a 500 mila. Li ho registrati alla lavagna, poi ho detto ai bambini che dovevamo contarle. Subito qualcuno ha proposto di fare fascetti da nove (sono abituati ai fascetti, perchè per distribuire velocemente le cannucce le teniamo legate con l'elastico in mazzetti da 9 o 10), abbiamo discusso un po' su questo numero e alla fine abbiamo deciso insieme di fare fascetti da 10, perchè 10 sono le dita delle nostre mani. Dopo aver fatto i fascetti da 10 cannucce, ho proposto di fare dei fascettoni da 10 fascetti, cioè da 100 cannucce. In questo modo siamo riusciti ad arrivare al numero totale delle cannucce, cioè 507. Ha vinto la sfida Gaia, che aveva detto 500.

Significati matematici che si vogliono costruire (tratto dalle guide del Progetto PerContare)
Si vuole arrivare al concetto di decina come raggruppamento di dieci oggetti (eventualmente anche astratti). La rappresentazione, dunque, che ci prefiggiamo di mediare è quella di una collezione di oggetti, in questo caso cannucce, in cui la numerosità è proprietà caratterizzante. È molto importante che la rappresentazione sia concreta e tangibile, e che gli oggetti (cannucce) di ogni fascetto-decina siano facilmente ricontabili ogni qualvolta ce ne sia il bisogno. L’elastico che stringe il fascetto potrà eventualmente essere visto come segno che caratterizza i fascetti-decina e che quindi ha come semantica la decina. Infine è importante ricordare che il numero 10 è così “speciale” solo perché il nostro sistema numerico è decimale, e questo deriva probabilmente dal fatto che abbiamo 10 dita, ma è soltanto una convenzione.

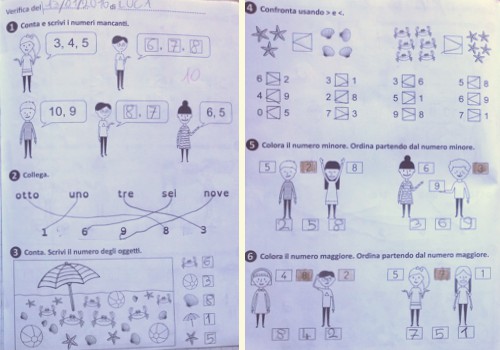
Come attività successiva ho proposto la verifica del 1° quadrimestre concordata con tutte le maestre delle classi prime dell'IC XX Settembre, che contiene esercizi su: contare avanti e indietro, associare numero e parola, contare oggetti, confrontare oggetti e numeri con > e <, ordinare una breve sequenza dal minore al maggiore e dal maggiore al minore.

Infine i bambini hanno svolto individualmente il problema del vaso di fiori contenuto in questa scheda.

Prosegue il lavoro sul calcolo mentale utilizzando il counting on. Abbiamo svolto due problemi di una nuova scheda.  

Oggi pomeriggio abbiamo di nuovo lavorato sul calcolo mentale con la tecnica del counting on e abbiamo svolto gli ultimi due problemi di questa scheda, seguendo lo stesso metodo di ieri.

Poi ho proposto questo lavoro, che viene utilizzato nel metodo Singapore. Ho dato a ogni bambino un fascetto di cannucce. Sul quaderno hanno disegnato tre schemi vuoti di legami numerici; alla lavagna ho scritto il numero che rappresenta il tutto e uno dei numeri che rappresentano le parti. Abbiamo preso le cannucce corrispondenti al tutto (il numero 7, in questo caso), abbiamo tolto le cannucce della prima parte e abbiamo scritto nella casella del legame numerico il numero mancante, corrispondente alle cannucce rimaste. Infine, abbiamo costruito una catena di operazioni che hanno tutte lo stesso risultato.

I due gruppi successivi sono stati eseguiti individualmente e corretti alla lavagna. Alcuni hanno incontrato qualche difficoltà, perchè "aggiungevano" la parte al tutto, invece di "togliere".

I compiti online per le vacanze sono stati eseguiti molto bene.

Questa mattina abbiamo lavorato sul calcolo mentale, sempre con il metodo del counting on. Ad es.: 6+5, partiamo da 6 e aggiungiamo 5 contando sulle dita. La maggior parte dei miei alunni sembra saper utilizzare questo metodo, solo pochi hanno bisogno di più esercizio, che faremo in ogni occasione possibile.

Ho presentato i problemi di addizione con le immagini. Avendo già lavorato sulle immagini con i legami numerici, i bambini hanno capito immediatamente come rappresentare con l'addizione adatta la situazione presentata nell'immagine. Ho utilizzato i primi tre disegni di questa scheda e ho proceduto come nei due esempi fotografati qui sotto.